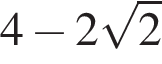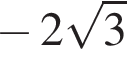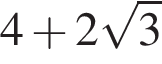Выберите три верных утверждения, если известно, что  и
и 
1) 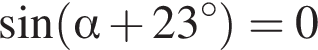
2) 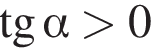
3) 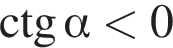
4) ![]() — угол первой четверти
— угол первой четверти
5) 
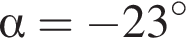
6) 
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 234.

Выберите три верных утверждения, если известно, что  и
и 
1) 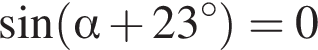
2) 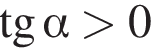
3) 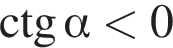
4) ![]() — угол первой четверти
— угол первой четверти
5) 
6) 
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 234.
Решение. Так как 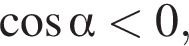 а
а 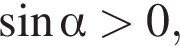 то
то 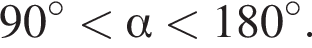 Заметим, что
Заметим, что  откуда
откуда 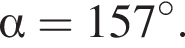 Тогда
Тогда 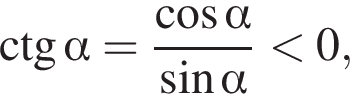 так как
так как ![]() — угол второй четверти. Пятое утверждение верно в силу основного тригонометрического тождества. Так как
— угол второй четверти. Пятое утверждение верно в силу основного тригонометрического тождества. Так как  то первое утверждение является верным.
то первое утверждение является верным.
Ответ: 135.

Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
| Начало предложения | Окончание предложения | |
| А) Значение выражения Б) Значение выражения В) Значение выражения | 1) 2) 3) 4) 2,5 5) 6) 5 |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Решение. A) Вынесем общий множитель за скобки и применим основное тригонометрическое тождество:
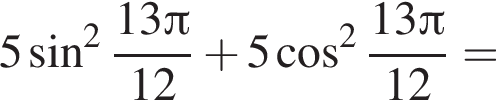
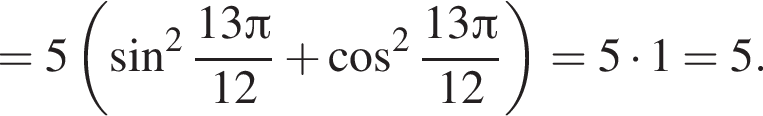
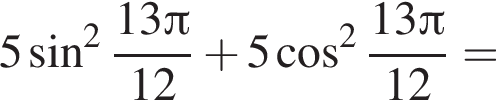
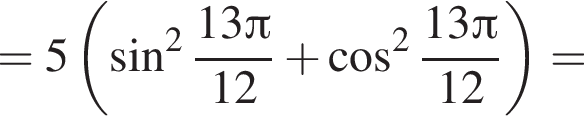
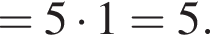
Б) Применим формулу синуса двойного аргумента:
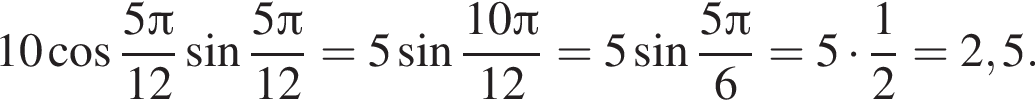

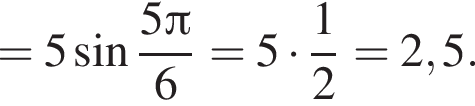
В) Применим формулу косинуса двойного аргумента:
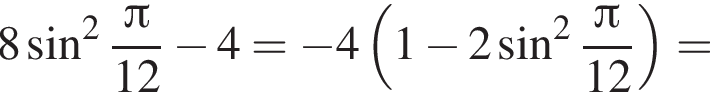
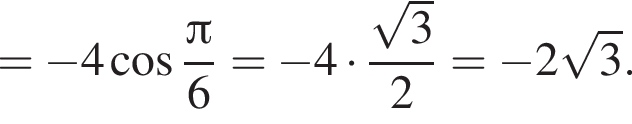
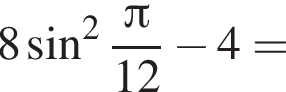
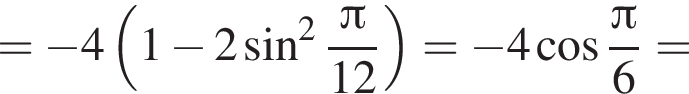
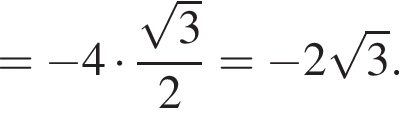
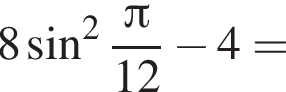
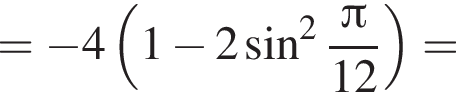
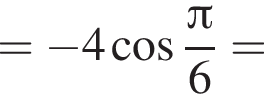
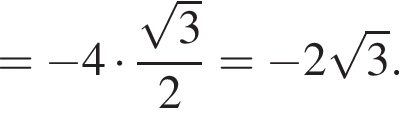
Ответ: А6Б4ВЗ.

Значение выражения 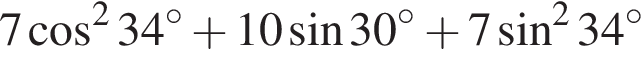 равно:
равно:
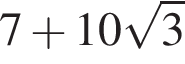
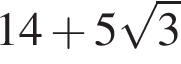
Решение. Имеем:

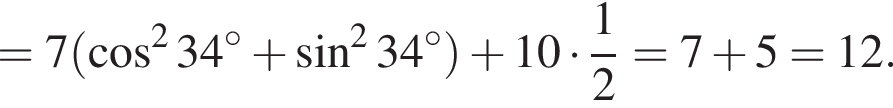

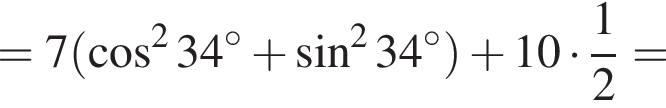
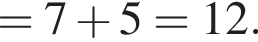
Правильный ответ указан под номером 1.

Найдите значение выражения 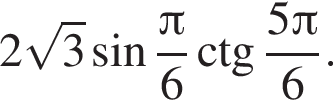
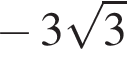
Решение. Вычислим:
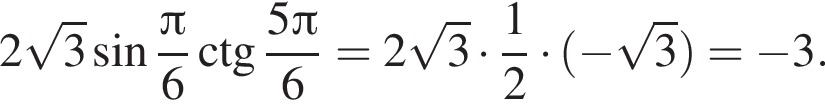
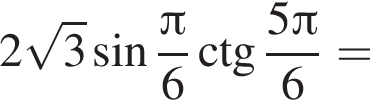
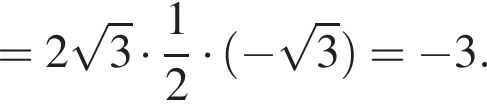
Правильный ответ указан под номером 1.

Найдите значение выражения 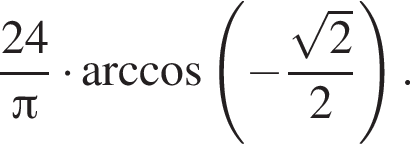
Решение. Найдем значение выражения:
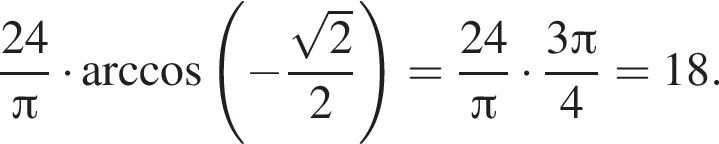
Ответ: 18.

Найдите значение выражения 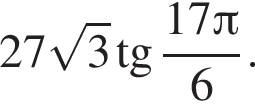
Решение. Найдем значение выражения:
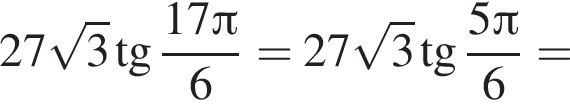
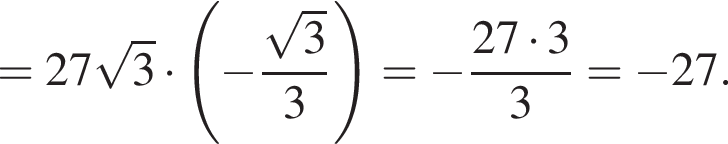
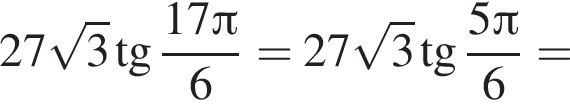
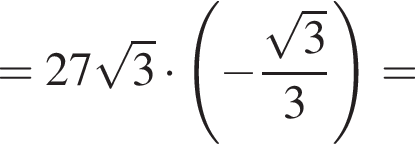
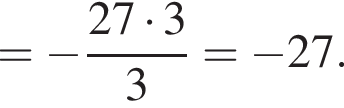
Ответ: −27.

Найдите значение выражения 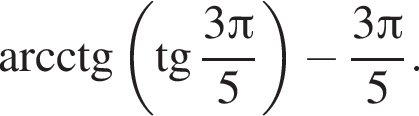
Решение. Заметим, что  только для
только для  Поэтому преобразуем, используя формулы приведения:
Поэтому преобразуем, используя формулы приведения:
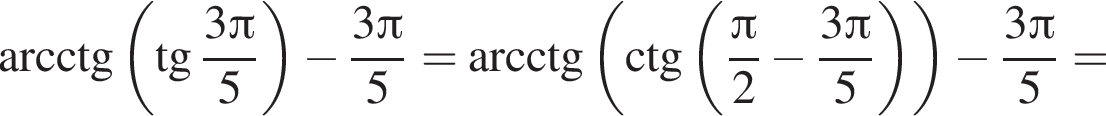
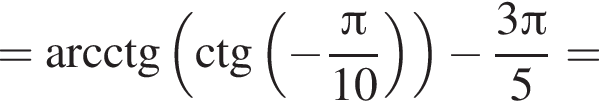
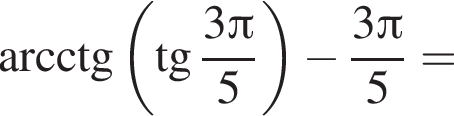
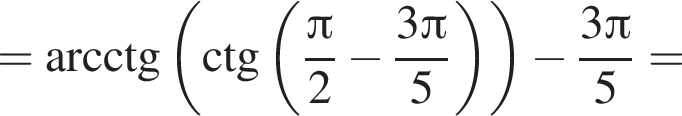
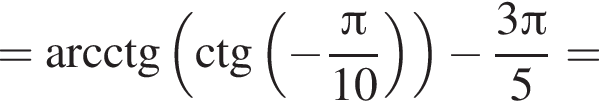
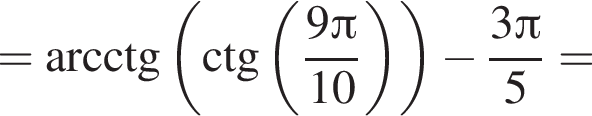
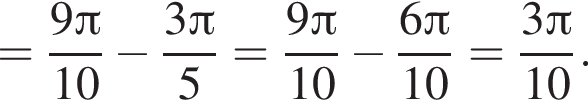
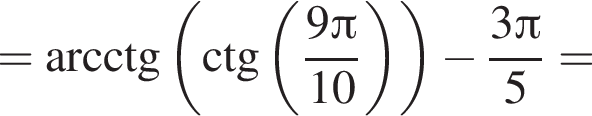
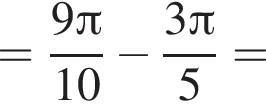
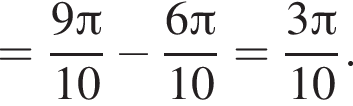
Правильный ответ указан под номером 5.

Найдите значение выражения 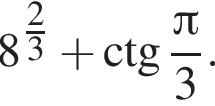
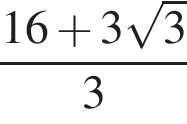
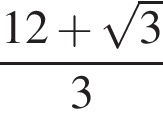
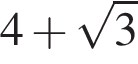
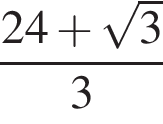

Решение. Найдем значение выражения:
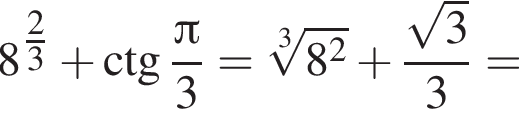
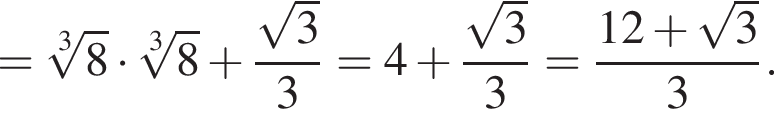
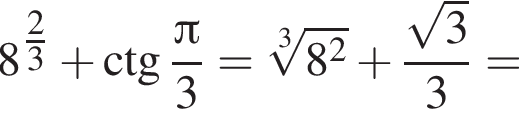
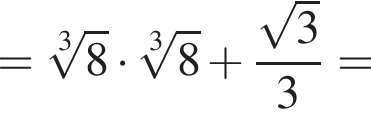
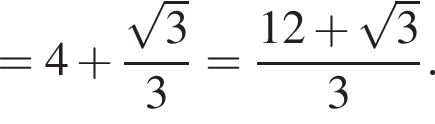
Правильный ответ указан под номером 2.

Найдите значение выражения 
Решение. Найдем значение выражения:
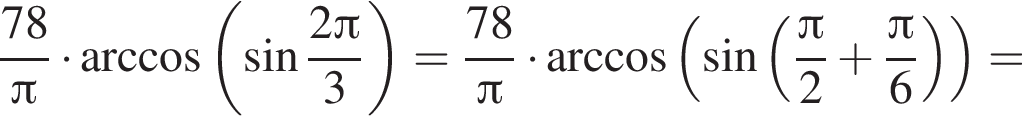
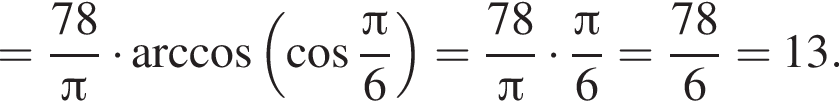
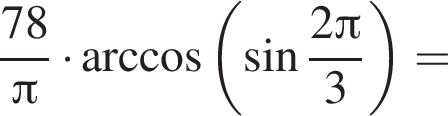
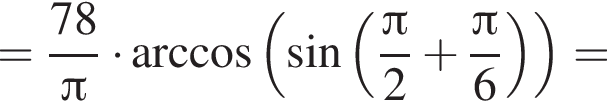
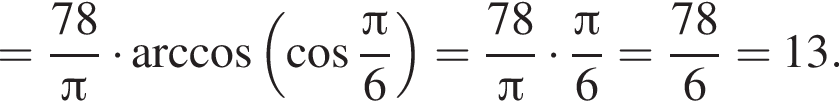
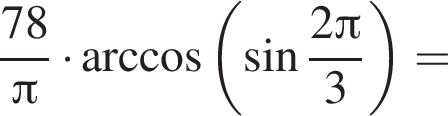
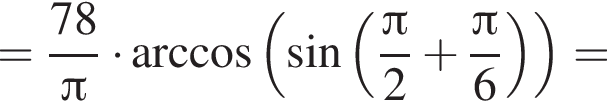
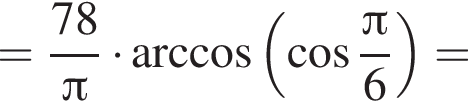
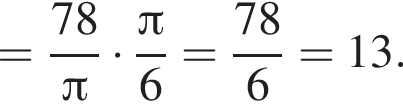
Ответ: 13.

Найдите значение выражения: 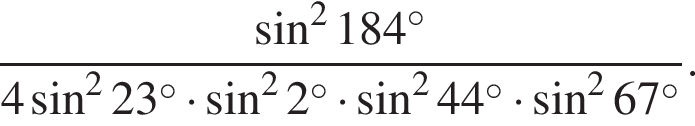
Решение. Используем формулы приведения:
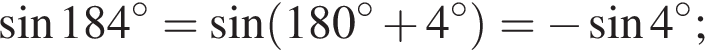

Используем формулу 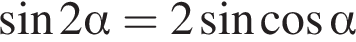 :
:

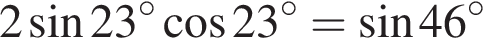
Поэтому имеем:
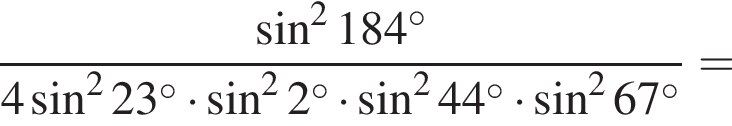
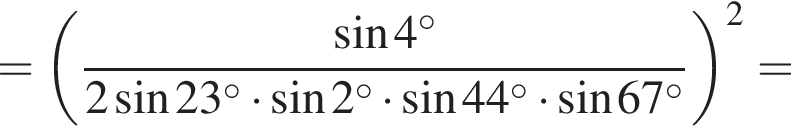
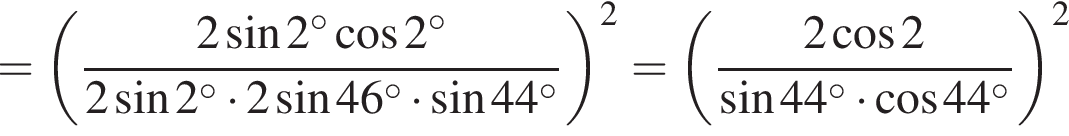
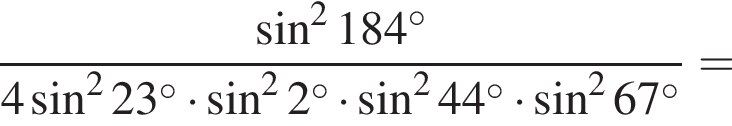
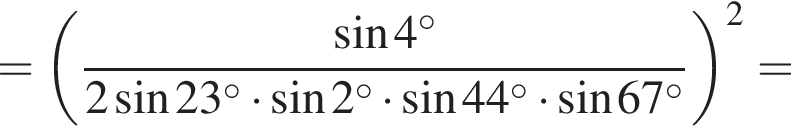
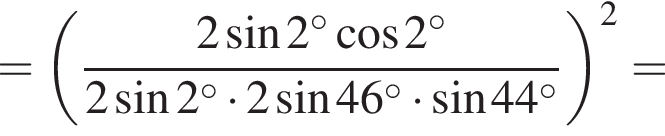
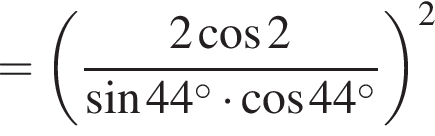
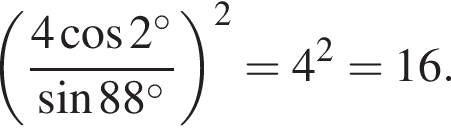
Ответ: 16.

Найдите значение выражения 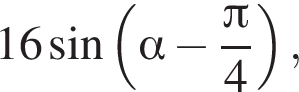 если
если 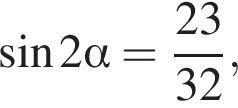
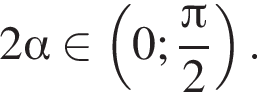
Решение. Заметим, что 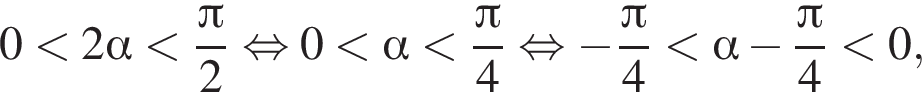 поэтому синус отрицателен. Далее имеем:
поэтому синус отрицателен. Далее имеем:

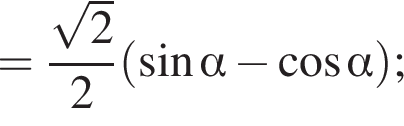
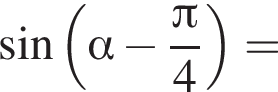
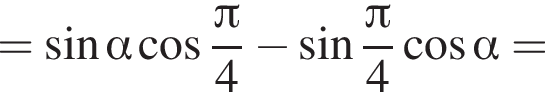
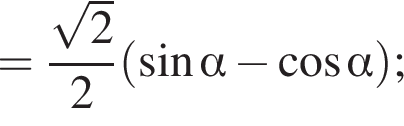
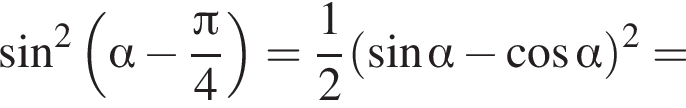
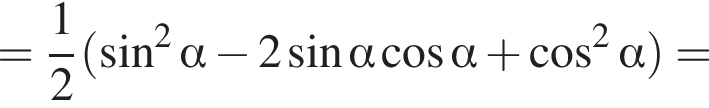
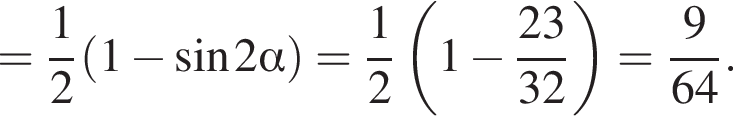
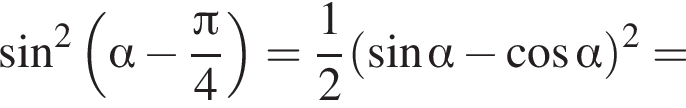
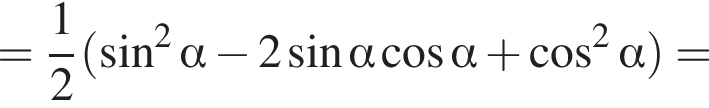
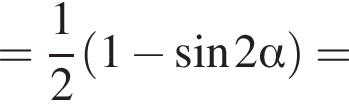
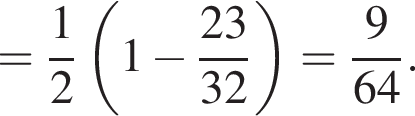
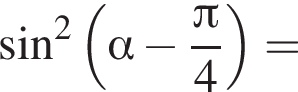
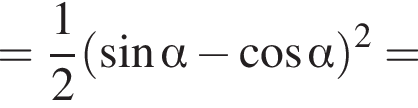
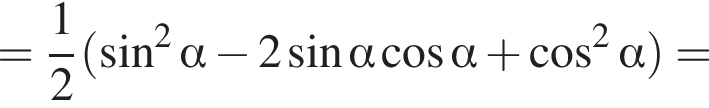
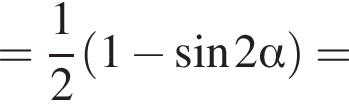
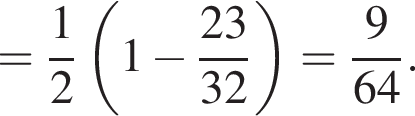
Тогда:
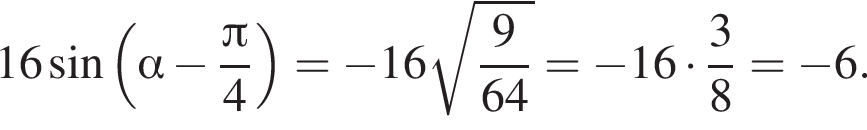
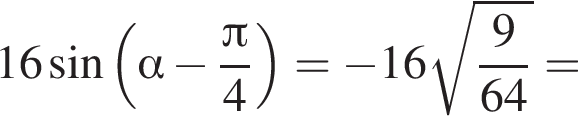
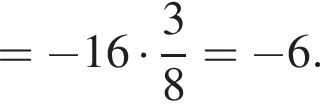
Ответ: −6.

Если 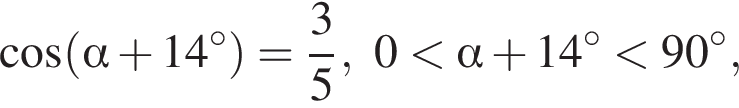 то значение выражения
то значение выражения 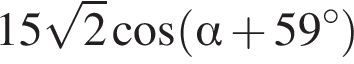 равно ...
равно ...
Решение. Обозначим 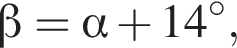 следовательно,
следовательно, 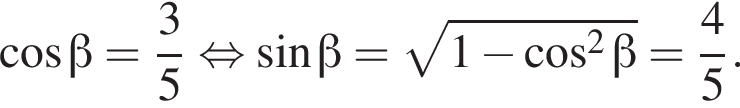 Заметим, что
Заметим, что  Таким образом:
Таким образом:
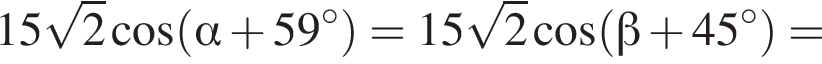
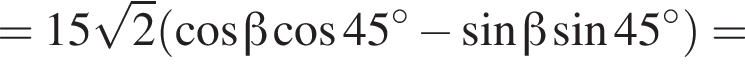
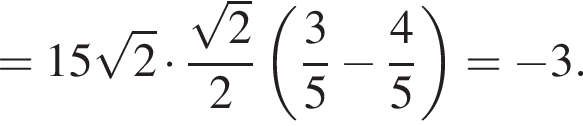
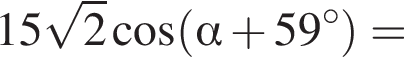
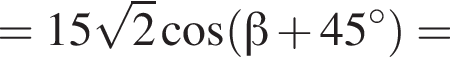
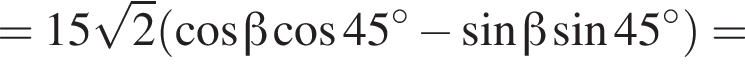
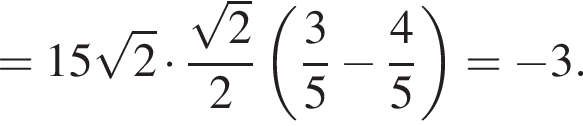
Ответ: −3.

Найдите значение выражения 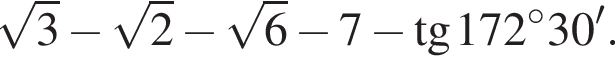
Решение. Преобразуем тангенс: 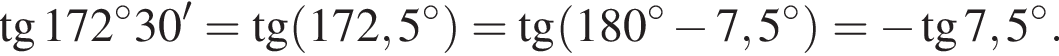
Воспользуемся формулой 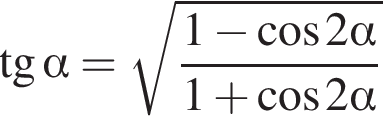 :
: 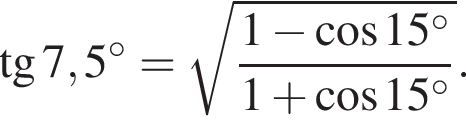
В свою очередь,




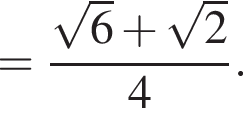
Поэтому:
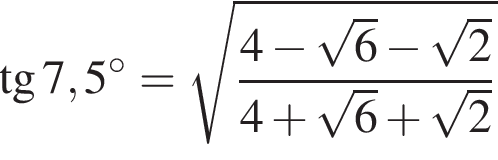
Домножим числитель и знаменатель на 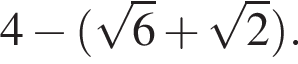 Тогда:
Тогда: 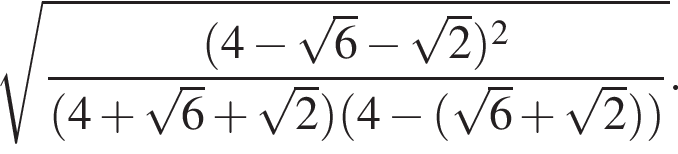
Так как 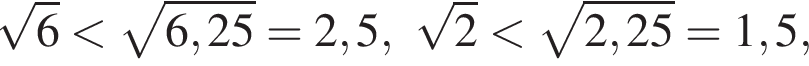 имеем
имеем  тогда
тогда 
Заметим, что в знаменателе 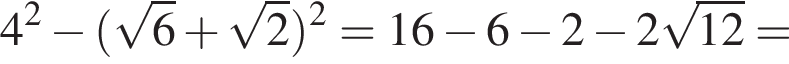
 Поэтому
Поэтому 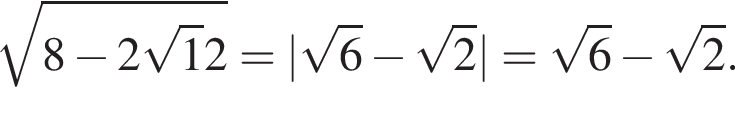 Тогда:
Тогда:
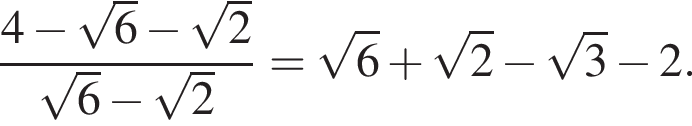
Тогда, подставляя в исходное выражение: 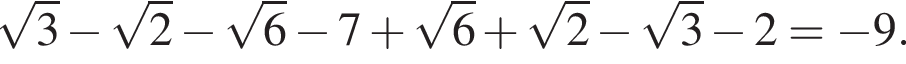
Ответ: −9.

Найдите значение выражения ![]() если
если 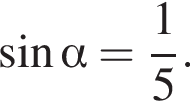
Решение. Имеем:

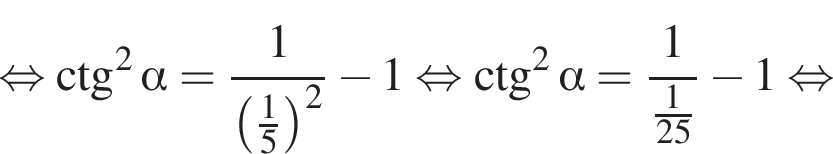
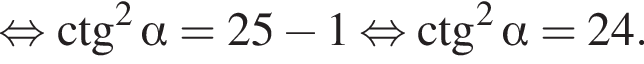
Ответ: 24.

Значение выражения 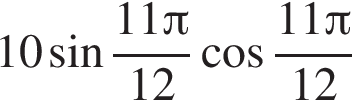 равно:
равно:
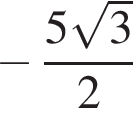
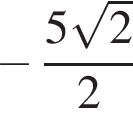
Решение. Воспользуемся формулой синуса двойного угла:
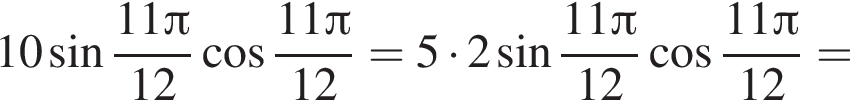
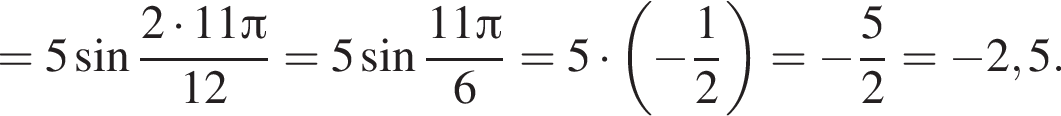
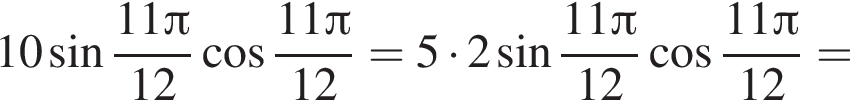
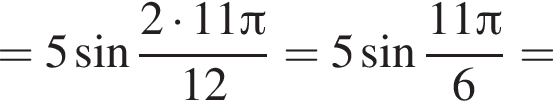
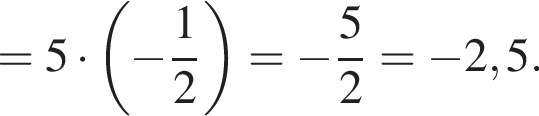
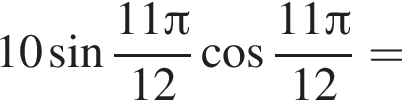
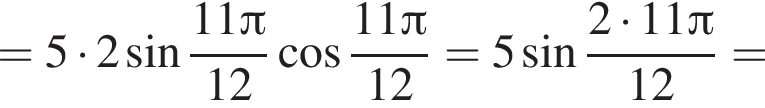

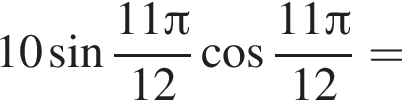
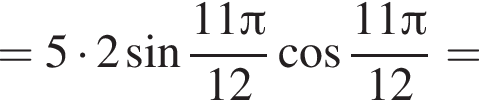
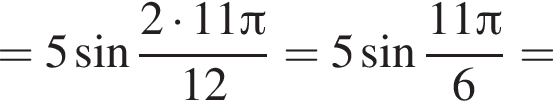
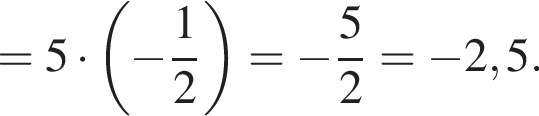
Ответ:

Найдите значение выражения 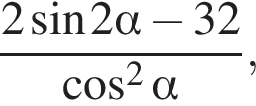 если
если 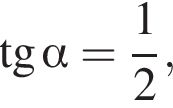
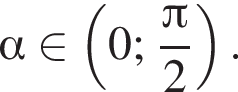
Решение. На указанном промежутке косинус в нуль не оборачивается. Воспользуемся формулой синуса двойного угла и разделим на косинус:
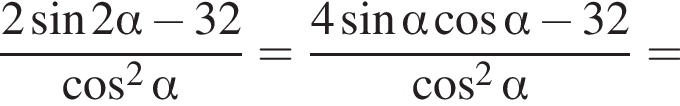
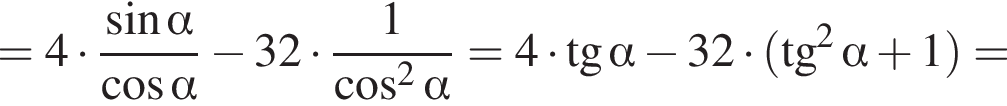
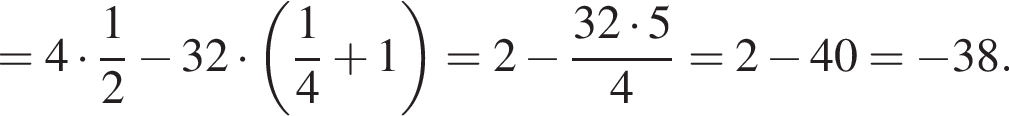
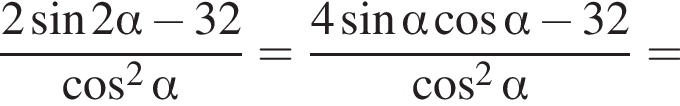
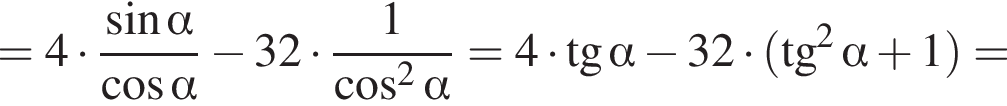
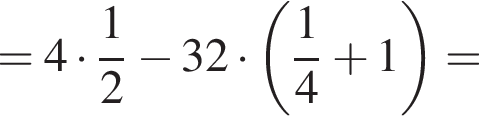
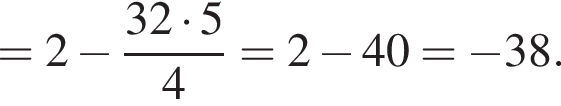
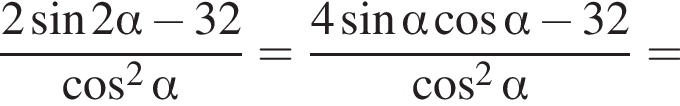
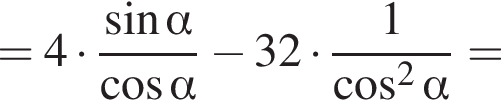
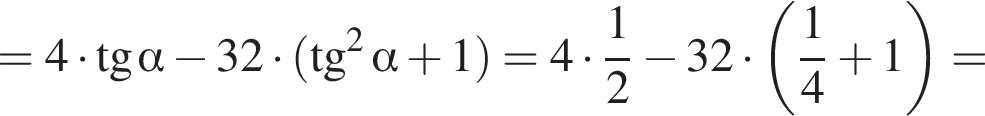
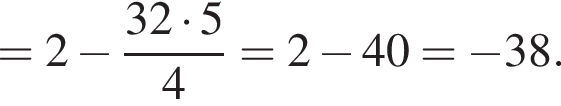
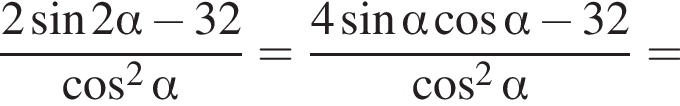
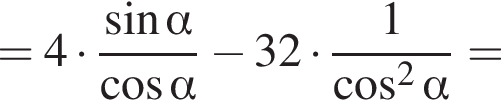
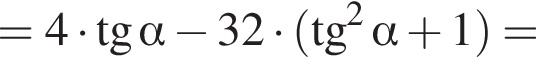
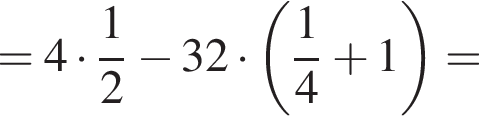
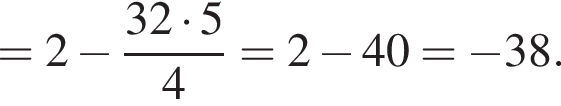
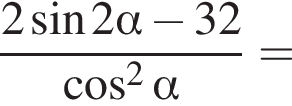
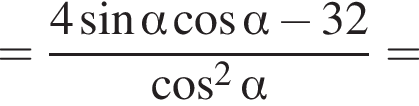
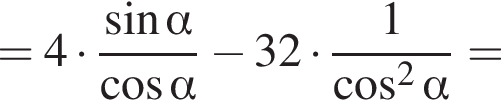
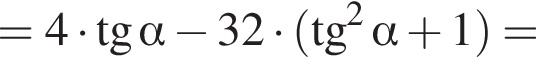
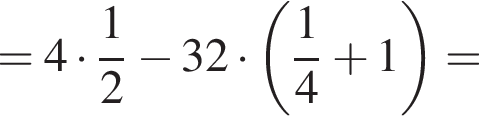
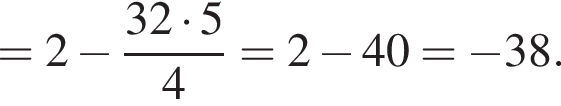
Ответ: − 38.
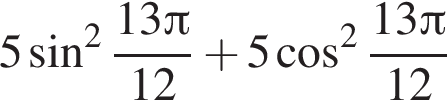 равно ...
равно ...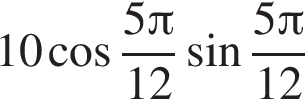 равно ...
равно ...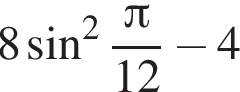 равно ...
равно ...